In the provocative concepts of morphogenetic fields and morphic resonance, we may indeed be more than the sum of our parts; we may have access to all that has gone before. Rupert Sheldrake, a biochemist, has postulated an extraordinary new theory which, if correct, could overturn our fundamental concepts about nature, brain function and consciousness. The theory suggests there may be mechanisms in evolution, as yet unrecognized by any science, other than those governed by ordinary natural selection.

In Seven Experiments That Could Change the World: A Do-It-Yourself Guide to Revolutionary Science, Sheldrake proposes an Alice Through the Looking Glass vision of things that possibly could be so but, in all probability, are not. Doing science in a controlled and thoughtful manner is a challenging and tricky operation. This is especially true of research on the paranormal, where the claims are difficult to prove because the effects are small and unreliable. Sheldrake advocates the collective participation of amateurs and nonscientists who have the "freedom to explore new areas of research." It is certainly true that the theories and methods of science change slowly and at times scientists do appear reluctant to accept new paradigms.

Become a member of Sheldrake's "army of revolutionary scientific experimenters."

The art of mathematics begins when you understand the theory of numbers... 1. Fermat's little theorem might have said that the congruence a^n+1= a (mod n) holds for all a if n is prime. Can you describe the set of integers n for which this property is in fact true? 2. Can you prove or disprove: for every odd number k there is a prime of the form 2^n k+1 3. Can you show that if (a^2 + b^2)/(ab+1) (for a,b in N) is integral, then it is a perfect square. Show that you know al little about Algebra ... 1. Why is it that there is no ring (= commutative, with 1) with exactly five units? 2. If a group has only finitely many elements of finite order, how do these form a subgroup? 3. Given: Let P and S denote the direct product and direct sum of countably many copies of Z, respectively, i.e. P is the set of all sequences of integers (a1, a2, a3, ... ) with the abelian group structure given by componentwise addition, and S is the subgroup consisting of all sequences with a subi = 0 for i sufficiently large. Describe how Hom subZ(P, Z) is isomorphic to S. That you know how to use Polynomials ... 1. Associate to a prime the polynomial whose coefficients are the decimal digits of the prime (e.g. 9 x^3 + 4 x^2 + 3 for the prime 9403). Show that this polynomial is always irreducible. 2. Suppose that b subn x^n + b subn-1 x^n-1 + ... + b sub1 x + b sub0 in R[x] has only real roots. Show that the polynomial b subn/n! x^n + b subn-1/(n-1)! x^n-1 + ... + b sub1/1! x + b sub0, has the same property. 3. Let p = 2m - 1 be an odd prime. Show that the polynomial (1-x)^m + 1 + x^m is twice a square in F subp[x]. and basic structural Geometry ... 1. Let A and B be two adjacent vertices of an equilateral polygon. If the angles at all other vertices are known to be rational (when measured in degrees), show that the angles at A and B are also rational. Give a counterexample to this statement when A and B are not assumed to be adjacent. 2. A rectangle R is the union of finitely many smaller rectangles (non-overlapping except on their boundaries), each one of which has at least one rational side. Show that R has the same property. 3. Mark an angle a (0 < a < 2 ) on a pie-plate, and pick another angle b (0 < b < 2 ). Define an operation on the pie as follows: cut out the slice of pie over the marked angle, lift it up, turn it over, replace it, and rotate the whole pie on the plate by the angle b. Can you show how, whatever the values of a and b, this operation has finite order (i.e., after a finite number of iterations every piece of the pie is in its original position). Finally, defining some sequences and recursions ... 1. Given: sequence t1, t2, t3, ... by the recursion tn+5 = (tn+4 tn+1 + tn+3 tn+2)/tn with initial values (1,1,1,1,1). Prove the statement that all of the tn are integral 2. Define a sequence u1, u2, u3, ... 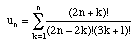by the formula Show that the statement "none of the un are integral" is false, but that the first counterexample is approximately 102019025. 3. Define a sequence v1, v2, v3, ... by the recursion vn =(2+v12 + ... + vn-12)/n. Show that the statement "all of the vn are integral" is false, but that the first counterexample is approximately 10178485291567. Problems and Conjectures Third International Conference Permutation Patterns May 24, 2005 Choice and chance;: An elementary treatise on permutations, combinations and probabilities with 300 exercises by William Allen Whitworth" Companion Chapter 18: Bootstrap Methods and Permutation Tests : for The Practice of Business Statistics by David S. Moore, et al Mathematics GCE A: Combinations, Permutations and Probabilities by Anthony Nicolaides (Paperback - 1994)" Permutation Methods: A Distance Function Approach.(Book Reviews)(Book Review) : An article from: Technometrics [HTML] by Shin Ta Liu (Digital) Updated Saturday, 27 May 2005 Experimenter's Review of the Physical Constants Henri Bergson by Jacques Chevalier William James and Henri Bergson: A Study in Contrasting Theories of Life by Horace M. Kallen New Science of Life: The Hypothesis of Formative Causation Sacred Universe (with Matthew Fox) Cassette Tape Seven Experiments That Could Change the World, Riverhead Books, 1996 The Physics of Angels, (with Matthew Fox), Harpercollins, 1996 Trialogues on the Edge of the West (with R. Abraham and T. McKenna), Bear and Co., 1992. The Evolutionary Mind More Books on Math and Philosophy Tuesday, June 21, 2005 By the Association for Research on Math And Science Association for Research on Teaching ARMS/ART Experimenter's Review of the Physical Constants